コンピュータの内部事情

前回からの続きです

https://tarosky.co.jp/tarog/7033

第２問については、コンピュータでの計算は基本的に２進数でビットの反転とビットシフト演算しか行えないので加算と減算はあまり区別されないということについてです。
参考のURLがそのままそうなんですけれどもプログラムの形で実装しました。

https://yttm-work.jp/computer_basics/computer_basics_0006.html

仕様としては8bitの計算機で入力された２つの数についての四則演算をするものになります。

足し算

def addition(a,b):#加算器
    x=[0,0,0,0,0,0,0,0]
    for i in range(8):
        j=7-i
        if 0<j:
            x[j-1]=a[j]&b[j]|x[j]&a[j]|x[j]&b[j]
        x[j]=x[j]^a[j]^b[j]
    return x

6行目と7行目がなにやら小難しいことをやっているように見えますけれど
6行目はその桁の2つの数と繰り上がりを足して2以上であれば繰り上がりをしますよという部分です。高校数学的に書くと、数値に1つ目と2つ目をA,B、繰り上がりをCとして
AかつBまたはCかつAまたはCかつBならば繰り上がりに１を代入する
という書き方です。
7行目はその桁の排他論理和、ようするに1が1つなら1、2つなら繰り上がりして0、3つなら繰り上がりして1というわけです。

負の数（正確には２の補数を作る関数）

def negate(a):#負の数を作る関数
    x=[0,0,0,0,0,0,0,0]
    for i in range(8):
        if a[i]==1: #今回は整数型で実装してしまったのでif文で代用しています。
            x[i]=0
        else:
            x[i]=1
    x=addition(x,[0,0,0,0,0,0,0,1])
    return x

全ての桁で0と1を入れ替えて一番下の桁に1を足すだけです。

左シフトの関数

def Lshift(a,b): #aからbの数だけ左シフトする
    x=[0,0,0,0,0,0,0,0]
    for i in range(8):
        if i<8-b:
            x[i]=a[i+b]
        else:
            x[i]=0
    return x

掛け算

def multiply(a,b):#乗算、実際のところ桁ごとに加算しているだけ
    x=[0,0,0,0,0,0,0,0]
    y=[0,0,0,0,0,0,0,0]
    for i in range(8):
        j=7-i
        if 0<b[j]:
            y=Lshift(a,i)
            x=addition(x,y)
    return x

割り算

#整数型の場合は何回引き算できるかで判別するのがよいかと
def divide(a, b):
    count=[0,0,0,0,0,0,0,0]
    mod=0
    aa=a
    nb=negate(b)
    while aa[0]<1:
        count=addition(count,[0,0,0,0,0,0,0,1])
        aa=addition(aa,nb)
    
    mod = addition(aa,b)
    count=addition(count,[1,1,1,1,1,1,1,1])
    return [count,mod]

2進数での負の数の表記方法にはいくつか種類があるのですけれど今回はざっくりやるので負の数については考慮していません。

実行部分

memo_a=[0,0,0,0,0,1,0,1]

memo_b=[0,0,0,0,0,0,1,1]

print("aの値")
print(memo_a)
print("bの値")
print(memo_b)
print("a+bの結果")
print(addition(memo_a,memo_b))
print("-bの値")
print(negate(memo_a))
print("aの左2シフトの結果")
print(Lshift(memo_a,2))
print("a*bの結果")
print(multiply(memo_a,memo_b))
print("a/bの結果")
print(divide(memo_a,memo_b))

実行結果

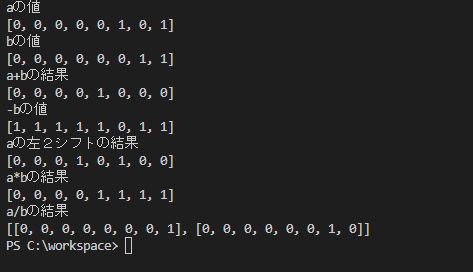
2進数表記での計算結果が出ました。やっていることは元の記事と同じではあるのですけれど、２進数での計算というのは内部的にはこういう感じですよということです。